Глава 12.1. Статистические распределения

Фундаментальным понятием математической статистики является понятие случайного числа (случайной величины). Согласно определению, случайная величина принимает то или иное значение, но какое конкретно — зависит от принципиально непредсказуемых обстоятельств опыта и заранее точно предсказано быть не может. Можно лишь говорить о вероятности Р(хк) принятия случайной дискретной величиной того или иного значения х_k или о вероятности попадания непрерывной случайной величины в тот или иной числовой интервал (х,х+Δх). Вероятность Р(х_k) или P(х)(Δх) соответственно может принимать значения от о (такое значение случайной величины совершенно невероятно) до i (случайная величина заведомо примет значение от х до (х+Δх). Соотношение Р(х_k) называют законом распределения случайной величины, а зависимость P(х) между возможными значениями непрерывной случайной величины и вероятностями попадания в их окрестность называется ее плотностью вероятности (probability density).

Глава 12.1.1. Статистические функции

В Mathcad имеется ряд встроенных функций, задающих используемые в математической статистике законы распределения. Они вычисляют как значение плотности вероятности различных распределений по значению случайной величины х, так и некоторые сопутствующие функции. Все они, по сути, являются либо встроенными аналитическими зависимостями, либо специальными функциями. Большой интерес представляет наличие генераторов случайных чисел, создающих выборку псевдослучайных данных с соответствующим законом распределения, что является основой методов Монте-Карло (см. разд. 12.2).

В Mathcad заложена информация о большом количестве разнообразных статистических распределений, включающая, с одной стороны, табулированные функции вероятности, и, с другой, возможность генерации последовательности случайных чисел с соответствующим законом распределения. Для реализации этих возможностей имеются четыре основных категории встроенных функций. Их названия являются составными и устроены одинаковым образом: первая литера идентифицирует определенный закон распределения, а оставшаяся часть (ниже в списке функций она условно обозначена звездочкой) задает смысловую часть встроенной функции:

d* (x,par) — плотность вероятности; р*(х,раг) — функция распределения; q*(P,par) — квантиль распределения; r* (M,раr) — вектор м независимых случайных чисел, каждое из которых имеет соответствующее распределение:

х — значение случайной величины (аргумент функции); Р — значение вероятности; par — список параметров распределения.

Чтобы получить функции, относящиеся, например, к равномерному распределению, вместо * надо поставить unif и ввести соответствующий список параметров par. Он будет состоять в данном случае из двух чисел: а,b — границ интервала распределения случайной величины.

Перечислим все типы распределения, реализованные в Mathcad, вместе с их параметрами, на этот раз обозначив звездочкой * недостающую первую букву встроенных функций. Некоторые из плотностей вероятности показаны на рис. 12.1.

*beta (x, s1, s2) — бета-распределение (s1, s2>0 — параметры, 0<x<1). *binom(k,n,p) — биномиальное распределение (n — целый параметр, 0<k<n и 0<р<1 — параметр, равный вероятности успеха единичного испытания).

Рис. 12.1. Плотность вероятности некоторых распределений

*cauchy(x,l,s) — распределение Коши (l — параметр разложения, s>0 — параметр масштаба). *chisq(x,d) — χ² ("хи-квадрат") распределение (d>0 — число степеней свободы). *ехр(х,r) — экспоненциальное распределение (r>0 — показатель экспоненты). *F(x,d1,d2) — распределение Фишера (d1,d2>0 — числа степеней свободы). *gamma(x,s) — гамма-распределение (s>0 — параметр формы). *geom(k,p) — геометрическое распределение (0<р<1 — параметр, равный вероятности успеха единичного испытания). *hypergeom(k,a,b,n) — гипергеометрическое распределение (а,b,n — целые параметры). *lnorm(х,µ, σ) — логарифмически нормальное распределение (µ— натуральный логарифм математического ожидания, σ>0 — натуральный логарифм среднеквадратичного отклонения). *logis (х,l,s) — логистическое распределение (1 — математическое ожидание, s>0 — параметр масштаба). *nbinom(k,n,p) — отрицательное биномиальное распределение (n>0 — целый параметр, 0<р<1). *norm(х,µ, σ) — нормальное распределение (µ— среднее значение, σ>0 — среднеквадратичное отклонение). *pois (k,λ) — распределение Пуассона (λ>0 — параметр). *t (x,d) — распределение Стьюдента (d>0 — число степеней свободы). *unif (х,а,b) — равномерное распределение (а<b — фаницы интервала). *weibuii (x, s) — распределение Вейбулла (s>0 — параметр).

ПРИМЕЧАНИЕ

Математический смысл каждой из четырех типов функций будет объяснен в следующем разделе на примере распределения Гаусса.

Вставку рассмотренных статистических функций в программы удобно осуществлять с помощью диалогового окна Insert Function (Вставка функции). Для этого необходимо выполнить следующие действия:

1. Установите курсор на место вставки функции в документе.

2. Вызовите диалоговое окно Insert Function нажатием кнопки f(x) на стандартной панели инструментов, или командой меню Insert / Function (Вставка / Функция), или нажатием клавиш <Ctrl>+<E>.

3. В списке Function Category (Категория функции) (рис. 12.2) выберите одну из категорий статистических функций. Категория Probability Density (Плотность вероятности) содержит встроенные функции для плотности вероятности, Probability Distribution (Функция распределения) — для вставки функций или квантилей распределения, Random Numbers (Случайные числа) — для вставки функции генерации случайных чисел.

4. В списке Function Name (Имя функции) выберите функцию в зависимости от требующегося закона распределения. При выборе того или иного элемента списка в текстовых полях в нижней части окна будет появляться информация о назначении выбранной функции.

5. Нажмите кнопку ОК для вставки функции в документ.

Рис. 12.2. Диалоговое окно Insert Function

Глава 12.1.2. Пример: нормальное (Гауссово) распределение

В теории вероятности доказано, что сумма различных независимых случайных слагаемых (независимо от их закона распределения) оказывается случайной величиной, распределенной согласно нормальному закону (так называемая центральная предельная теорема). Поэтому нормальное распределение хорошо моделирует самый широкий круг явлений, для которых известно, что на них влияют несколько независимых случайных факторов.

Перечислим еще раз встроенные функции, имеющиеся в Mathcad для описания нормального распределения вероятностей:

dnorm(x,µ, σ) — плотность вероятности нормального распределения; pnorm(х,µ,σ) —функция нормального распределения; сnorm(х) — функция нормального распределения для µ=0,σ=1; qnorm(P,µ,σ) — обратная функция нормального распределения; rnorm(M,µ, σ) — вектор м независимых случайных чисел, каждое из которых имеет нормальное распределение:

х — значение случайной величины; P — значение вероятности; µ — математическое ожидание; σ — среднеквадратичное отклонение.

Математическое ожидание и дисперсия являются, по сути, параметрами распределения. Плотность распределения для трех пар значений параметров показана на рис. 12.3. Напомним, что плотность распределения dnorm задает вероятность попадания случайной величины х в малый интервал от х до х+Δх. Таким образом, например, для первого графика (сплошная линия) вероятность того, что случайная величина х примет значение в окрестности нуля, приблизительно в три раза больше, чем вероятность того, что она примет значение в окрестности х=2. А значения случайной величины большие 5 и меньшие -5 и вовсе очень маловероятны.

Рис. 12.3. Плотность вероятности нормальных распределений

Рис. 12.4. Нормальные функции распределения

Функция распределения F(x) (cumulative probability) — это вероятность того, что случайная величина примет значение, меньшее или равное х. Как следует из математического смысла, она является интегралом от плотности вероятности в пределах от -∞ до х. Функции распределения для упомянутых нормальных законов изображены на рис. 12.4. Функция, обратная F(x) (inverse cumulative probability), называемая еще квантилем распределения, позволяет по заданному аргументу р определить значение х, причем случайная величина будет меньше или равна х с вероятностью р.

ПРИМЕЧАНИЕ

Здесь и далее графики различных статистических функций, показанные на рисунках, получены с помощью Mathcad без каких-либо дополнительных выражений в рабочей области.

Приведем несколько примеров, позволяющих почувствовать математический смысл рассмотренных функций на примере случайной величины х, распределенной по нормальному закону с µ=0 и σ=1 (листинги 12.1—12.5).

Листинг 12.1. Вероятность того, что х будет меньше 1.881

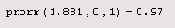
Листинг 12.2. 97-% квантиль нормального распределения

Листинг 12.3. Вероятность того, что х будет больше 2

Листинг 12.4. Вероятность того, что х будет находиться в интервале (2,3)

Листинг 12.5. Вероятность того, что |x|<2

Обратите внимание, что задачи двух последних листингов решаются двумя разными способами. Второй из них связан с еще одной встроенной функцией erf, называемой функцией ошибок (или интегралом вероятности, или функцией Крампа).

erf(x) — функция ошибок. erfc(x)=1-erf(x).

Математический смысл функции ошибок ясен из листинга 12.5. Интеграл вероятности имеет всего один аргумент, в отличие от функции нормального распределения. Исторически последняя пересчитывалась через табулированный интеграл вероятности по формулам, приведенным в листинге 12.6 для произвольных значений параметров µ и σ(листинг 12.6).

Листинг 12.6. Вероятность того, что х будет в интервале (2,3)

Если вы имеете дело с моделированием методами Монте-Карло, то в качестве генератора случайных чисел с нормальным законом распределения применяйте встроенную функцию rnorm. В листинге 12.7 ее действие показано на примере создания двух векторов по M=500 элементов в каждом с независимыми псевдослучайными числами x1_i и х2_i распределенными согласно нормальному закону. О характере распределения случайных элементов векторов можно судить по рис. 12.5. В дальнейшем мы будем часто сталкиваться с генерацией случайных чисел и расчетом их различных средних характеристик.

Листинг 12.7. Генерация двух векторов с нормальным законом распределения

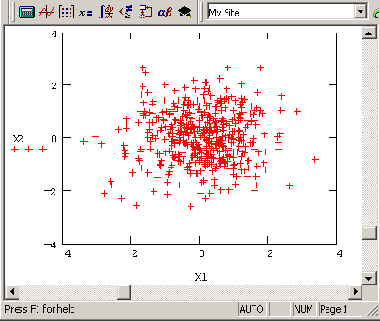
Рис. 12.5. Псевдослучайные числа с нормальным законом распределения (продолжение листинга 12.7)

Глава 12.2. Выборочные статистические характеристики

В большинстве статистических расчетов вы имеете дело с выборками: либо со случайными данными, полученными в ходе какого-либо эксперимента (которые выводятся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, рассмотренными в предыдущих разделах встроенными функциями, моделирующими то или иное явление методом Монте-Карло (см. разд. 12.3). Рассмотрим возможности Mathcad по оценке функций распределения и расчету числовых характеристик случайных данных.

Глава 12.2.1. Гистограммы

Гистограммой называется график, аппроксимирующий по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b) разбивается на некоторое количество bi_n сегментов, а затем подсчитывается процент попадания данных в каждый сегмент. Для построения гистограмм в Mathcad имеется несколько встроенных функций. Рассмотрим их, начиная с самой сложной по применению, чтобы лучше разобраться в возможностях каждой из функций.

Гистограммы с произвольными интервалами

hist (intvls,x) — вектор частоты попадания данных в интервалы гистограммы:

intvls — вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания a<intvls_i<b; х — вектор случайных данных.

Если вектор intvls имеет bin элементов, то и результат hist имеет столько же элементов. Построение гистограммы иллюстрируется листингом 12.8 и рис. 12.6.

Листинг 12.8. Построение гистограммы

Для анализа взято N=1000 данных с нормальным законом распределения, созданных генератором случайных чисел (третья строка листинга). Далее определяются границы интервала (upper, lower), содержащего внутри себя все случайные значения, и осуществляется его разбиение на количество (bin) одинаковых сегментов, начальные точки которых записываются в вектор int (предпоследняя строка листинга).

ПРИМЕЧАНИЕ

В векторе int можно задать произвольные границы сегментов разбиения так, чтобы они имели разную ширину.

Рис. 12.6. Построение гистограммы (продолжение листинга 12.8)

Обратите внимание, что в последней строке листинга осуществлена нормировка значений гистограммы, с тем чтобы она правильно аппроксимировала плотность вероятности, также показанную на графике.

Гистограммы с равными интервалами

Если нет необходимости задавать сегменты гистограммы разной ширины, то удобнее воспользоваться упрощенным вариантом функции hist:

hist (bin, х) — вектор частоты попадания данных в интервалы гистограммы:

bin — количество сегментов построения гистограммы; х — вектор случайных данных.

Для того чтобы использовать этот вариант функции hist вместо предыдущего, достаточно заменить первый из ее аргументов в листинге 12.8 следующим образом:

Недостаток упрощенной формы функции hist в том, что по-прежнему необходимо дополнительно определять вектор сегментов построения гистограммы.

От этого недостатка свободна функция histogram:

histogram (bin, х) — матрица гистограммы размера binx2, состоящая из столбца сегментов разбиения и столбца частоты попадания в них данных:

bin — количество сегментов построения гистограммы; х — вектор случайных данных.

Примеры использования функции histogram приведены в листинге 12.9 и на рис. 12.7. Сравнение с предыдущим листингом подчеркивает простоту построения гистограммы этим способом (стоит отметить, что в листинге 12.9, в отличие от предыдущего, мы не нормировали гистограмму).

Листинг 12.9. Упрощенный вариант построения гистограммы

Рис. 12.7. График и матрица гистограммы (продолжение листинга 12.9)

ПРИМЕЧАНИЕ

Для того чтобы назначить двумерному графику тип гистограммы, в диалоговом окне Formatting Currently Selected Graph (Форматирование) установите на вкладке Traces (Графики) тип списка bar (Столбцы) или solidbar (Гистограмма). На рис. 12.6 и 12.7 применены установки второго типа: закрашенными столбиками (solidbar).

Глава 12.2.2. Среднее и дисперсия

В Mathcad имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных:

mean(x) — выборочное среднее значение; median (х) — выборочная медиана (median) — значение аргумента, которое делит гистограмму плотности вероятностей на две равные части; var (х) — выборочная дисперсия (variance); stdev(x) — среднеквадратичное (или стандартное) отклонение (standard deviation); max(x) ,min(x) — максимальное и минимальное значения выборки; mode(x) — наиболее часто встречающееся значение выборки; var(х),stdev(x) — выборочная дисперсия и среднеквадратичное отклонение в другой нормировке:

х — вектор (или матрица) с выборкой случайных данных.

Пример использования первых четырех функций приведен в листинге 12.10.

Листинг 12.10. Расчет числовых характеристик случайного вектора

Определение статистических характеристик случайных величин приведено в листинге 12.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, вы без труда освоите связь между встроенными функциями.

ВНИМАНИЕ!

Осторожно относитесь к написанию первой литеры в этих функциях, особенно при обработке малых выборок (листинг 12.11).

Листинг 12.11. К определению статических характеристик

Иногда в статистике встречаются и иные функции, например, помимо арифметического среднего, применяются другие средние значения:

gmean(x) — геометрическое среднее выборки случайных чисел; hmean(x) — гармоническое среднее выборки случайных чисел.

Математическое определение этих функций и пример их использования в Mathcad приведены в листинге 12.12.

Листинг 12.12. Вычисление различных средних значений

Глава 12.2.3. Примеры: Выборочная оценка дисперсии и среднего нормальной случайной величины

Типовые задачи математической статистики связаны с получением тех или иных интервальных и точечных оценок различных параметров случайной выборки. Приведем пример двух задач, иллюстрирующих назначение и принципы применения введенных в предыдущих разделах статистических функций.

Интервальная оценка дисперсии

Требуется определить числовой интервал (L,U), внутри которого будет лежать с вероятностью 1-а=75% дисперсия нормальной случайной величины, исходя из объема выборки в N чисел. Эта задача решается в статистике с помощью χ²-распределения (листинг 12.13).

Листинг 12.13. Интервальное оценивание дисперсии

Указанный интервал называется (1-a) доверительным интервалом. Обратите внимание на использование при решении данной задачи функции stdev (с прописной буквы) для расчета выборочного стандартного отклонения. В статистике часто встречаются выражения, которые более удобно записывать через функции в такой нормировке, именно для этого они и появились в Mathcad.

Проверка статистических гипотез

В статистике рассматривается огромное число задач, связанных с проверкой тех или иных гипотез н. Разберем пример простой гипотезы. Пусть имеется выборка N чисел с нормальным законом распределения и неизвестными дисперсией и математическим ожиданием. Требуется принять или отвергнуть гипотезу H о том, что математическое ожидание закона распределения равно некоторому числу µ0=0. 2.

Задачи проверки гипотез требуют задания уровня критерия проверки гипотезы а, который описывает вероятность ошибочного отклонения истинной н. Если взять ее очень малым, то гипотеза, даже если она ложная, будет почти всегда приниматься; если, напротив, взять а близкими 1, то критерий будет очень строгим, и гипотеза, даже верная, скорее всего, будет отклонена.

В нашем случае гипотеза состоит в том, что µ0=0.2, а альтернатива— что µ0#0.2. Оценка математического ожидания, как следует из курса классической статистики, решается с помощью распределения Стьюдента с параметром N-1 (этот параметр называется степенью свободы распределения).

Для проверки гипотезы (листинг 12.14) рассчитывается (а/2)-квантиль распределения Стьюдента т, который служит критическим значением для принятия или отклонения гипотезы. Если соответствующее выборочное значение T по модулю меньше т, то гипотеза принимается (считается верной). В противном случае гипотезу следует отвергнуть.

Листинг 12.14. Проверка гипотезы о математическом ожидании при неизвестной дисперсии

В последней строке листинга вычисляется истинность или ложность условия, выражающего решение задачи. Поскольку условие оказалось ложным (равным не 1, а 0), то гипотезу необходимо отвергнуть.

На рис. 12.8 показано распределение Стьюдента с N-l степенью свободы, вместе с критическими значениями, определяющими соответствующий интервал. Если t (оно тоже показано на графике) попадает в него, то гипотеза принимается; если не попадает (как произошло в данном случае) — отвергается. Если увеличить а, ужесточив критерий, то границы интервала будут сужаться по сравнению с показанными на рисунке.

Рис. 12.8. К задаче проверки статистических гипотез (продолжение листинга 12.14)

В листинге 12.15 приводится альтернативный способ проверки той же самой гипотезы, связанный с вычислением значения не квантиля, а самого распределения Стьюдента.

Листинг 12.15. Другой вариант проверки гипотезы (продолжение листинга 12.14)

Мы разобрали только два характерных примера статистических вычислений. Однако с помощью Mathcad легко решаются самые разнообразные задачи математической статистики.

ПРИМЕЧАНИЕ

Большое количество задач разобрано в Ресурсах в рубрике Statistics (Статистика) Быстрых шпаргалок.

Глава 12.2.4. Корреляция

Функции, устанавливающие связь между парами двух случайных векторов, называются ковариацией и корреляцией (или, по-другому, коэффициентом корреляции). Они различаются нормировкой, как следует из их определения (листинг 12.16):

соrr(х) — коэффициент корреляции двух выборок; cvar(x) — ковариация двух выборок:

x1,x2— векторы (или матрицы) одинакового размера с выборками случайных данных.

Листинг 12.16. Расчет ковариации и корреляции

ПРИМЕЧАНИЕ

Как видно, полученное значение корреляции близко к нулю, т. е. псевдослучайные числа генерируются практически независимо. О том, как создать массив коррелированных чисел, написано ниже (см. разд. 12.3.2).

Глава 12.2.5. Новые функции корреляционного анализа сигналов

В Mathcad 12 появились две функции, связанные с корреляционной обработкой сигналов и изображений:

correl(x,y) — вектор, представляющий значения коэффициента ковариации двух векторов; correl2d(A,K) — матрица, равная ковариации матрицы-аргумента и матрицы-окна:

х,у — векторы; А — матрица-прототип; K — матрица-окно (размера, меньшего чем А).

Смысл действия одномерной функции correl заключается в последовательном сдвиге одного вектора относительно другого, перемножении и суммировании их элементов, стоящих в таком положении друг напротив друга. Это не совсем ковариация в терминах математической статистики, поскольку не осуществляется нормировки (деления полученной суммы на число перемноженных элементов). Работа двумерной функции correl2d состоит в последовательном позиционировании "маленькой" матрицы (окна) на фоне "крупной" (прототипа), перемножении их элементов, находящихся друг над другом, и суммировании их. В результате получается элемент матрицы корт реляции, соответствующий центрам наложения матрицы-прототипа и матрицы-окна. Обе эти функции играют определенную роль в задачах обработки сигналов.

Глава 12.2.6. Коэффициенты асимметрии и эксцесса

Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящей через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например, нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.

Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной — коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.

Для расчета коэффициентов асимметрии и эксцесса в Mathcad имеются две встроенные функции:

kurt (х) — коэффициент эксцесса (kurtosis) выборки случайных данных х; skew(x) — коэффициент асимметрии (skewness) выборки случайных данных X.

Примеры расчета коэффициентов асимметрии и эксцесса для распределения Вейбулла приведены в листинге 12.17.

Листинг 12.17. Расчет выборочных коэффициентов асимметрии и эксцесса

Глава 12.2.7. Статистические функции матричного аргумента

Все рассмотренные примеры работы статистических функций относились к векторам, элементы которых были случайными числами. Но точно так же все эти функции применяются и по отношению к выборкам случайных данных, сгруппированных в матрицы. При этом статистические характеристики рассчитываются для совокупности всех элементов матрицы, без разделения ее на строки и столбцы. Например, если матрица имеет размерность MxN, то и объем выборки будет равен M-N.

Соответствующий пример вычисления среднего значения приведен в листинге 12.18. В его первой строке определяется матрица данных х размера 4x2. Действие встроенной функции mean матричного аргумента (последняя строка листинга) иллюстрируется явным суммированием элементов матрицы х (предпоследняя строка). Действие прочих встроенных функций на матрицы совершенно аналогично действию их на векторы (листинг 12.19).

Листинг 12.18. Вычисление среднего значения элементов матрицы

Листинг 12.19. Действие различных статистических функций на матрицу

ПРИМЕЧАНИЕ

Некоторые статистические функции (например, вычисления ковариации) имеют два аргумента. Они также могут быть матрицами, но, в соответствии со смыслом функции, должны иметь одинаковую размерность.

Большинству статистических функций позволяется иметь в качестве аргументов даже не одну матрицу, а любое количество матриц, векторов и скаляров. Числовые характеристики будут рассчитаны для всей совокупности значений аргументов функции. Соответствующий пример приведен в листинге 12.20.

Листинг 12.20. Статистические функции нескольких аргументов

Глава 12.3. Методы Монте-Карло

Для моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло, обязанные своим названием европейскому центру азартных игр, основанных на случайных событиях. Основная идея этих методов состоит в создании определенной последовательности случайных чисел, моделирующей тот или иной эффект, например, шум в физическом эксперименте, случайную динамику биржевых индексов и т. п. Фактически все содержание предыдущего раздела (см. разд. 12.2) являлось примером реализации методов Монте-Карло, поскольку содержало расчет тех или иных статистических характеристик имитационных данных, полученных при помощи генератора случайных чисел.

Рассмотрим еще несколько типовых задач, относящихся к методам Монте-Карло, попутно изучая соответствующие возможности, заложенные в Mathcad.

Глава 12.3.1. Генерация псевдослучайных чисел

Как уже отмечалось (см. разд. 12.1.1), для генерации M-компонентного вектора независимых псевдослучайных чисел имеется ряд встроенных функций, реализующих различные типы статистических распределений и имеющих вид r*(M,раr), где * — идентификатор, a par— список параметров конкретного распределения. В частности, генератор нормальных псевдослучайных чисел был рассмотрен ранее (см. разд. 12.1.2), а для равномерного распределения предусмотрено две встроенных функции:

runif (M,а,b) — вектор м независимых случайных чисел, каждое из которых имеет равномерное распределение; rnd(x) — случайное число, имеющее равномерную плотность распределения на интервале (0,х):

х — значение случайной величины; Р — значение вероятности; (а,b) — интервал, на котором случайная величина распределена равномерно.

Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad — дань традиции, применяемой в большинстве сред программирования. Возможно, именно скалярный тип этой функции определяет простоту и привычность ее использования в расчетах моделей типа Монте-Карло.

Рис. 12.9. Модель сигнал/шум с равномерным законом распределения

Рис. 12.9 демонстрирует широко распространенный прием моделирования, основанный на смеси некоторого полезного сигнала f(х) и шумовой компоненты а, что характерно для типичного физического эксперимента. В качестве шума используется серия равномерно распределенных псевдослучайных чисел. Различные соотношения интенсивностей сигнала и шума определяют различные условия модельной задачи и позволяют эффективно протестировать алгоритмы, которые разработаны для ее решения.

ПРИМЕЧАНИЕ

Более сложные статистические расчеты для модели сигнал/шум приведены в листинге 12.24 (см. разд. 12.3.4).

Параметры генераторов псевдослучайных чисел

В Mathcad применяются типичные алгоритмы генерации последовательностей псевдослучайных чисел, которые используют в качестве "отправной точки" некоторое начальное (или отправное) значение (seed value). Это начальное значение используется для того, чтобы совершить над ним определенные математические действия (к примеру, взять остаток от деления на некоторое другое число) и получить в итоге первое псевдослучайное число последовательности. Затем те же математические операции совершаются с первым числом для получения второго, и т. д.

Несложно догадаться, что если использовать все время одно и то же начальное значение генератора псевдослучайных чисел, то, открывая всякий раз новый документ со встроенной функцией получения тех или иных псевдослучайных чисел, будет выдаваться в точности одна и та же их последовательность. Сами числа внутри последовательности будут "почти" случайными (значимость этого "почти" будет зависеть только от качества алгоритма генерации), но вот сама последовательность при каждом открытии документа будет одной и той же.

ПРИМЕЧАНИЕ

Вы можете сами убедиться в идентичности выдаваемых последовательностей псевдослучайных чисел, открывая и закрывая несколько раз документ с рис. 12.9 или любой документ с иным датчиком случайных чисел, описанных в данном разделе. Любопытным также будет эксперимент по последовательному применению нескольких встроенных функций генерации псевдослучайных чисел в пределах одного документа.

Для того чтобы иметь возможность поменять саму последовательность сгенерированных случайным датчиком чисел, в Mathcad 11 (и выше) предусмотрена новая возможность явного определения используемого им начального значения. Для этого вызовите командой меню Tools/ Worksheet Options (Сервис / Опции документа) диалог Worksheet Options (Опции документа) и на вкладке Built-in Variables (Встроенные переменные) введите желаемое (целое) число в поле ввода Seed value for random Bombers (Начальное значение для генератора псевдослучайных чисел).

Альтернативный способ заключается в использовании соответствующей встроенной функции непосредственно в документе:

seed(x) — функция установки нового начального значения для генератора псевдослучайных чисел:

х — новое начальное значение для генератора псевдослучайных чисел (целое число от 1 до 2147483647).

Глава 12.3.2. Генерация коррелированных выборок

До сих пор мы рассматривали наиболее простой случай применения генераторов независимых случайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией. Приведем пример программы, создающей два вектора x1 и х2 одинакового размера и одним и тем же распределением, случайные элементы которых попарно коррелированны с коэффициентом корреляции R (листинг 12.21).

Рис. 12.10. Псевдослучайные числа с корреляцией R=0.4 (продолжение листинга"12.21) и R=0.9

Листинг 12.21. Генерация попарно коррелированных случайных чисел

Результат действия программы для R=0.4 показан на рис. 12.10 (слева). Сравните полученную выборку с правым графиком, полученным для высокой корреляции (R=0.9) и с рис. 12.5 (см. разд. 12.1.2) для независимых данных, т. е. R=0.

Глава 12.3.3. Моделирование случайного процесса

Встроенные функции для генерации случайных чисел создают выборку из случайных данных A_i. Часто требуется создать непрерывную или дискретную случайную функцию A(t) одной или нескольких переменных (случайный процесс или случайное поле), значения которой будут упорядочены относительно своих переменных. Создать псевдослучайный процесс можно способом, представленным в листинге 12.22.

Листинг 12.22. Генерация псевдослучайного процесса

В первых строках листинга 12.22 определено количество N независимых случайных чисел, которые будут впоследствии сгенерированы, и радиус временной корреляции т. В следующих трех строках определяются моменты времени т,, которым будут отвечать случайные значения A(t_j). Создание нормального случайного процесса сводится к генерации обычным способом вектора независимых случайных чисел х и построению интерполяционной зависимости в промежутках между ними. В листинге 12.22 используется сплайн-интерполяция (см. главу 13).

В результате получается случайный процесс A(t), радиус корреляции которого определяется расстоянием т между точками, для которых строится интерполяция. График случайного процесса A(t) вместе с исходными случайными числами показан на рис. 12.11. Случайное поле можно создать несколько более сложным способом с помощью многомерной интерполяции.

ПРИМЕЧАНИЕ

Простой пример генерации двумерного случайного поля вы найдете на компакт-диске, прилагаемом к книге.

Рис. 12.11. Псевдослучайный процесс (продолжение листинга 12.22)

К случайным процессам, сгенерированным таким способом, как и к данным эксперимента, применяются любые статистические методы обработки, например, корреляционный или спектральный анализ. Приведем в качестве примера листинг 12.23, показывающий, как организовать расчет корреляционной функции случайного процесса.

Листинг 12.23. Дискретизация случайного процесса и вычисление корреляционной функции (продолжение листинга 12.19)

Дискретизация интервала (0,T_m_ах) для случайного процесса A(t) произведена с различным элементарным интервалом А (первая строка листинга). В зависимости от значения А получается различный объем n выборки случайных чисел Yi, являющихся значениями случайной функции A(t) в точках дискретизации. В последних четырех строках определяются различные характеристики случайной величины Y, являющиеся, по сути, характеристиками случайного процесса A(t). График рассчитанной в 2-М+1 точках корреляционной функции R(j) показан на рис. 12.12.

Рис. 12.12. Корреляционная функция (продолжение листингов 12.22—12.23)

ПРИМЕЧАНИЕ

Внимательному читателю предлагается самостоятельно ответить на вопрос: почему при таком расчете корреляционной функции её значение R (0) не равно 1, как должно быть по определению?

Глава 12.3.4. Пример: огибающая и фаза нормального случайного процесса

Завершим разговор о моделировании случайных процессов примером, часто встречающимся в задачах статистической радиофизики. Рассмотрим модель, представляющую собой сумму гармонической функции и нормально распределенной шумовой компоненты, которая хорошо описывает передачу сигнала в электронных устройствах в условиях помех (листинги 12.24—12.25) и называется узкополосным нормальным процессом. Как известно, узкополосный процесс представим в виде E(t)exp(iф(t)), где случайные функции E(t) и ф(t) называются, соответственно, его огибающей и фазой. Мы приведем пример нулевого сигнала (т. е. расчет огибающей и фазы чистого случайного процесса), хотя минимальное изменение листинга 12.25 даст вам возможность промоделировать и ненулевые значения сигнала.

Первая половина листинга 12.24 представляет собой подготовительный этап, заключающийся в генерации двух векторов с нормальным распределением вероятности. Из курса математической статистики известно, что узкополосный гауссов процесс можно представить в виде, приведенном в последней строке листинга 12.24, причем случайные функции A(t) и C(t) называются квадратурными составляющими нормального случайного процесса. Графики A(t) и C(t) показаны на рис. 12.13. Листинг 12.25 содержит суммирование полученных шумовых компонент с составляющими гармонического сигнала и выдает в качестве результата функции E(t) и ф(t) (они показаны на рис. 12.14).

Листинг 12.14. Квадратурные составляющие нормального случайного процесса

Рис. 12.13. Квадратурные составляющие случайного процесса (продолжение листинга 12.24)

Листинг 12.25. Огибающая и фаза нормального случайного процесса (продолжение листинга 12.24)

Рис. 12.14. Огибающая и фаза нормального случайного процесса (продолжение листингов 12.24—25)