Результаты моделирования
После того, как модель построена и введена вся необходимая информация, модель готова к работе. Запуск модели осуществляется либо открытием меню Simulation и выбором команды Start, либо нажатием кнопки Start/Pause Simulation, либо из командного окна MATLAB.
Окно и значения параметров блока Signal Generator
Примером скалярной последовательности может служить одноканальный сигнал, когда данные следуют одно за другим, то есть каждому временному отсчёту соответствует одно значение сигнала. Многоканальный сигнал, когда одному и тому же временному отсчёту соответствуют несколько значений, представляет собой векторную последовательность. Таким образом, скалярный сигнал задаётся вектором или одномерным массивом u (рис. 2а), в то время как векторный сигнал — матрицей U размерности MxN, в которой M строк соответствуют моментам времени 1, 2, ... M, а N значений k-ой строки представляют собой мгновенную выборку сигнала в момент времени k (рис. 2б).

Скалярные и векторные сигналы: а) скалярный сигнал; б)векторный сигнал
Окно параметров блока Variance показано на рис. 3. Блок предназначен для вычисления дисперсии входной последовательности данных и, в зависимости от параметра Running Variance, может работать в двух режимах: Basic Operation и Running Operation. Если этот параметр не включен, работа выполняется в режиме Basic Operation. В этом случае, если входная последовательность векторная, блок на каждом временном шаге вычисляет дисперсию текущей мгновенной выборки, если же входная последовательность скалярная, то, поскольку мгновенная выборка состоит из одного значения, выходом блока будет нуль.

Окно и значения параметров блока Variance
В нашем случае (рис. 3) параметр Running Variance включен. Это означает, что блок работает в режиме Running Operation. Если входной сигнал является скалярным, как это имеет место для обсуждаемой модели, дисперсия вычисляется на каждом временном шаге с учётом всех данных, поступивших на текущий момент времени, и отображается на пиктограмме блока Display. Другими словами, в процессе работы модели блок Variance вычисляет, а Display отображает число, изменяющееся с частотой следования данных и равное дисперсии сигнала на интервале от начального до текущего момента времени. Если входной сигнал векторный, и мгновенная выборка содержит N значений, блок на каждом временном шаге вычисляет N значений дисперсии.
Включение параметра Reset Port (установка флажка, как показано на рис. 3) приводит к появлению дополнительного входного порта Rst, показанного на пиктограмме блока под основным входом In. Порт Rst принимает скалярный входной сигнал. В момент, когда в порт поступает ненулевое значение, происходит сброс накопленных данных, и блок выдаёт нулевое значение дисперсии. Таким образом, использование порта Rst целесообразно, когда требуется управлять размером временного окна, на котором оценивается дисперсия входного сигнала. Переключая ключ Switch двойным щелчком левой клавиши мыши, можно осуществлять это управление.
Обратимся теперь к блоку Histogram, окно параметров которого и введённые значения показаны на рис. 4. Параметр Running Histogram определяет способ обработки входных данных, он аналогичен параметру Running Variance блока Variance. Целое число Number of bins задаёт количество бинов (столбцов) для расчёта гистограммы, а Minimum value of input и Maximum value of input определяют, соответственно, минимальное и максимальное значения, откладываемые по оси абцисс при расчёте и построении гистограммы. Выходом блока является векторный сигнал, размерность которого равна количеству столбцов гистограммы, а компоненты — высоте каждого из столбцов. Если установлен флажок Normalised, каждый выходной векторный отсчёт нормализуется к единице, то есть площадь гистограммы приводится к 1.

Окно и значения параметров блока Histogram
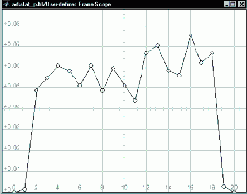
Построение гистограммы, динамически изменяющейся в соответствии с поступающими данными, выполняется блоком User-Defined Frame Scope. Форма отображения данных требует небольшого пояснения. На рис. 5 изображена гистограмма некоторого сигнала (серые столбики) и чёрная линия, представляющая собой результат соединения отрезками прямых середин вершин соседних столбиков (отмечены кружочками). В обсуждаемой модели простейшего АЦП (“Chip News”, № 2) блок User-Defined Frame Scope используется для построения таких кусочно-линейных функций по выходным сигналам блока Histogram. Следует обратить внимание на то, что по оси абцисс отложены номера интервалов группировки (начальный номер равен 0), а не границы этих интервалов.

Формирование графика блоком
Рассматриваемая модель содержит блоки Buffered FFT Frame Scope. Каждый из блоков вычисляет оценку СПМ дискретного сигнала по данным, находящимся в буфере. Окно параметров блока показано на рис. 6. Здесь длина последовательности, над которой выполняется преобразование Фурье, и длина буфера заданы как переменная N. Это означает, что в данном случае перед запуском модели в командном окне MATLAB необходимо присвоить этой переменной конкретное численное значение.

Окно и значения параметров блока Buffered FFT Frame Scope
Ряд блоков требует определения периода дискретизации (параметр Sample Time). Его можно задавать либо в численном виде, либо с помощью переменной, например, T. В последнем случае перед запуском модели параметр T должен быть определён в командном окне. Присвоение этому параметру значения “-1” приводит к тому, что данный блок автоматически устанавливает период дискретизации по входному сигналу. Автоматическое определение периода дискретизации возможно только тогда, когда буферизация данных выполняется без перекрытия (параметр Buffer overlap равен “0”), в противном случае, получаемые результаты будут некорректны.
После того, как параметры блоков модели определены, необходимо ввести информацию о начальном и конечном времени моделирования, методе численного интегрирования, используемого при расчёте протекающих процессов, шаге интегрирования и другие сведения, определяемые пользователем [1,2]. Для этого в окне модели надо открыть раздел Parameters, находящийся в меню Simulation, и ввести необходимые данные. На этом процедура построения модели заканчивается, и полученную модель необходимо сохранить, для чего следует воспользоваться командой Save или Save as в меню File.
Гистограмма шума квантования
Результаты моделирования представлены на следующих рисунках:
рис. 7 — гистограмма шума квантования; рис. 8 — СПМ сигнала; рис. 9 — СПМ шума округления; рис. 10 — фрагменты входного (светлая линия) и выходного (тёмная линия) сигналов АЦП.
СПМ шума квантования
При моделировании использовались следующие значения параметров: период дискретизации T — 2-10; длина буфера данных N — 256; разрядность n моделируемого АЦП — 12; пределы измерений ± A входного сигнала (вводится значение A) — 1; мощность шума (блок Band-Limited White Noise) — 10-3; шаг квантования (блок Quantezer) — 2·A/(2n); начальное и конечное время моделирования (start time и finish time в меню Simulation/Parameters) — соответственно, 0 и inf.

Фрагменты входного и выходного сигналов АЦП
Для оценки зависимости дисперсии шума квантования от разрядно-сти АЦП было выполнено моделирование для значений разрядности n от 2 до 12 включительно, результаты представлены на рис. 11. Из него видно, что увеличение количества разрядов на единицу ведёт к уменьшению дисперсии шума приблизительно на 6 дБ, что согласуется с известными теоретическими результатами.

Задание параметров модели
Следующим шагом после построения модели простейшего АЦП (“Chip News” № 2, стр. 5) является задание параметров входящих в неё блоков. Для этого надо дважды щёлкнуть левой клавишей мыши по выбранному блоку. В результате откроется окно, в котором показаны значения параметров, введённые ранее или установленные по умолчанию. В качестве примера на рис. 1 показано окно блока Signal Generator, в котором задана частота синусоидального сигнала, равная 128 Гц (по умолчанию — 1 Гц). Чтобы новые установки вступили в силу, после ввода параметров надо щёлкнуть по кнопке “Apply” или “OK”. Окно параметров каждого блока имеет кнопку “Help” для получения необходимой справочной информации, поэтому здесь мы ограничимся рассмотрением лишь некоторых блоков, представляющих интерес с точки зрения обработки сигналов, а именно, Variance, Histogram и Buffered FFT Frame Scope. Эти блоки, как, впрочем, большинство блоков библиотеки DSP, работают как со скалярными, так и с векторными последовательностями (скалярными и векторными дискретными сигналами).

Как было отмечено, одним из
Как было отмечено, одним из достоинств системы Simulink являются простота и гибкость процесса построения модели. По мере накопления опыта, пользователь несомненно оценит и другие возможности, делающие Simulink мощным инструментом по-строения, отладки и исследования моделей разнообразных динамических систем. Важной особенностью функциональных блоков системы (в том числе, и входящих в рассматриваемую модель) является их многофункциональность. В зависимости от заданных параметров, один и тот же блок может работать со скалярными или векторными сигналами, иметь или не иметь дополнительные входы и выходы и так далее. Например, в рассмотренной модели блок Signal Generator позволяет генерировать синусоидальные, пилообразные, прямоугольные и случайные сигналы. Изменяя параметры отдельных блоков при неизменной компоновке, можно моделировать системы с совершенно различными динамическими свойствами, что в полной мере относится и к модели, рассмотренной в статье.
Необходимые программные средства для проекта предоставлены фирмой SoftLine Corp.
Литература
1. Дьяконов В.П., Абраменкова И.В. MatLab 5.0/5.3. Система символьной математики. — М.: “Нолидж”. — 1999. — 633 с.
2. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows. Практич. пособие. — СПб.: КОРОНА принт. — 1999. — 288 с.
3. Потемкин В.Г. Система MATLAB. Справ. пособие. — Диалог-МИФИ. — 1997. — 350 с.
4. Потемкин В.Г. MATLAB 5 для студен-тов. — Диалог-МИФИ. — 1998. — 314 с.
5. Потемкин В.Г.
MATLAB 5 для студентов. — Диалог-МИФИ. — 1999. — 447 с.
6. Потемкин В.Г. Система инженерных и научных расчётов MATLAB 5.х. В 2-х томах. — Диалог-МИФИ. — 1999 (т. 1. — 366 с., т. 2. — 304 с.).
7. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования с примерами на языке МАТЛАБ: Учеб. Пособие под ред. проф. Фрадкова А.Л. — СПб.: БГТУ. — 1994. — 190 с.
8. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования. Издание 2 дополненное. — СПб.: БГТУ. — 1996. — 191 с.
9. Дьяконов В.П. Справочник по применению системы PC MatLAB. — М.: Наука, Физматлит. — 1993
